Home Page of RDScience
Kirchhoff's Rules For Circuits
Gustav Kirchhoff was one of those fiendishly clever people who made important discoveries in more than one area of science.
Here we are interested in his work on electrical circuits, not on spectroscopy or thermodynamics. This web page is dedicated to the
idea that although the laws are quite simple, it is very easy to mess up problems that use them.
Law 1
Kirchhoff's laws concern solving problems in electrical networks that contain voltage sources (idealised batteries) and resistors. This is a good idealisation
for real networks of batteries and resistors at steady state (no quickly switching things on or changing values of components).
Suppose that you go cross country skiing in Peter Lougheed Provincial park. It has an extensive network of trails and is very popular with skiers.
If you were to watch an intersection where several trails meet you would obviously see that the number of skiers skiing into an
intersection equals the numbers skiing out (ignoring the ones who have stopped to eat their sandwiches). If we apply this to electrons
at the junction in a circuit the same logic applies. The number of electrons flowing in (and therefore the current, which is just the rate of flow of electrons
expressed in eccentric units called amps) equals the number flowing out (and therefore the current flowing out). It is pretty obvious stuff.
Question 1
Suppose that a junction has 4 leads called a,b,c and d. In leads a and b current flows into the junction with values of 30mA and 120 mA respectively. In
lead c 180 mA flow out of the junction. What happens in lead D? Well the sums of the flow into the junction is zero. We can chose the convention that flow into
the junction is positive and flow out is negative (or we could do the reverse). So we can write:
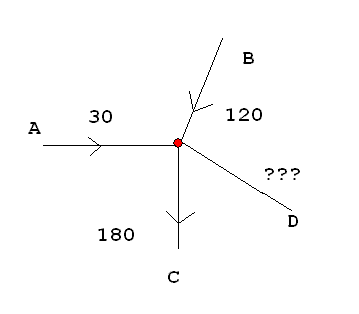
30 + 120 - 180 +d = 0
From which we find the d = +30. The positive value means (by the convention that we just chose) that a current (30 mA) flows into the junction.
Facetious Question 1
Suppose that you are the class troublemaker, and you ask your instructor about the possibility that electrons hang about at junctions and eat their sandwiches.
Is this possible? There are components where, at least temporarily, electrons hang about and this law does not apply. However, we stated at the beginning that the law applies only
to voltage sources and resistors, which have a strict "no sandwich" policy. The laws don't apply to quickly changing voltages (such as high frequency signals) where
properties such as "capacitance" permit all sorts of improper dalliances. In practical situations you need to ask whether heating might cause resistors to change their values, or whether
batteries can maintain their voltage at the required voltage. Also it generally requires a higher voltage to pass a current the 'wrong way' through a battery (pushing electrons in the negative terminal).
However this analysis does not recognise this.
Law 2
So you have parked your car, skied around many trails, and finally returned to your car. However far you have been, however, one thing is for certain:
the amount of up-hill (the total elevation gain) is equal to the total down-hill (the total elevation loss). Because you start and finish in the same place this must be so. We could
define 'uphill' and 'downhill' in terms of 'gravitational potential'. We know that if we move a fixed mass in a gravitational field you can convert energy into or from 'gravitational potential energy'
e.g. by skiing up hill or down hill with the mass. But the law of conservation of energy seems inviolable. In detail, the strength and direction of the gravitational field varies around mountains.
No matter, any ski trip where you end up where you started involves creating as much gravitational potential energy (slogging up hills) as you destroy (whizzing down hills). This, of course,
leads to the annoying sense of moral superiority that cross country skiers have over downhill skiers.
So where is this leading? Electrons, being charged, are subject to electrical fields, and thus acquire and loose electrical potential energy. So voltage is analogous to altitude. An electron returning to the same place must have exactly
the same amount of electrical potential energy and so the sum of the voltage changes in any loop must equal zero.
Assembling Voltages in a loop as an equation
We are going to look at a trivial case and we are going to work it out 4 different ways. Why? Because we have to be able to follow rules with the ardent conviction of
a recent convert to a religion, and not be swayed by what we can see is really happening.

So we have a loop with a battery and a resistor. We have three things that have direction around the loop:
- The 'loop direction'. This is indicated by the grey arrow. It is the direction that we choose to go when assembling the equations and it is arbitrary.
- The nominal current direction. I have put little arrows on the circuits, sometimes one way sometimes the other, and I have labelled them 'I'. In a more complicated example it won't always be obvious which way the current actually flows.
- The actual direction that the current flows. We are going to totally ignore this because it must come out of the answer that we derive.
Conventions
Some of these conventions are arbitrary. They are set up for dealing with conventional current rather than electron flow. I feel that this avoids an extra level of confusion.
- Usually the currents in the circuit are the unknowns (although it could also include battery voltages, or resistances if some currents are given). We need to write down a set of equations corresponding to loops that let us solve for the unknowns.
So there must be as many equations as unknowns and every unknown must feature somewhere in the set of equations (every component must be passed though by at least one loop).
- Each equation corresponds to a loop. We are going to list all the changes in voltage as we go round the loop and set the sum of these to zero.
- When we go through a battery (i.e.in our loop direction) if we go from -ve to +ve we register this as an increase in voltage, from +ve to -ve we have a negative change.
- When we go through a resistor then the voltage change is obtained from V=IR. But is it a +ve or -ve change? The rule we will use is that if the loop direction is the same as the nominal current direction then we subtract.
If they are opposite then we add.
So we are going to now do four versions of our trivial example. The idea is to see how by sticking to our conventions everything comes right in the end. In our trivial example we only have one loop, one unknown and one equation.
Version A
- We start by going from -ve to +ve through the battery (therefore from convention 3 we have a positive voltage change). The battery has a voltage of 6 so a + 6 is added to our equation.
- Next we go through the resistor. The loop direction is the same as the nominal current direction (the little arrow drawn to indicate current). So by convention 4 we write this as negative voltage change. As
We use V=IR and the resistance is 60 ohms we add the term -60I to the equation
- We have completed the loop, so we set the sum of our voltage changes to zero (law 2). And get the equation 6 - 60I = 0.
- We solve the equation to find that I = +0.1 amps. The positive value indicates that the conventional current flows in the direction of the nominal flow (the little arrow that I drew on the diagram)
Version B
This is the same as A except that we are going round the loop in the opposite direction.
- We start by going from +ve to 0-ve through the battery (therefore from convention 3 we have a negative voltage change). The battery has a voltage of 6 so a - 6 is added to our equation.
- Next we go through the resistor. The loop direction is now opposite to the nominal current direction (the little arrow drawn to indicate current). So by convention 4 we write this as positive voltage change. As
We use V=IR and the resistance is 60 ohms we add the term +60I to the equation
- We have completed the loop, so we set the the terms for voltage change to zero (law 2). We get the equation -6 + 60I = 0.
- Again We solve the equation to find that I = +0.1 amps. The positive value indicates that the conventional current flows in the direction of the nominal flow (the little arrow that I drew on the diagram indicating clockwise current is positive)
Version C
This is the same as A except that I have made the nominal current direction go the other way
- We start by going from -ve to +ve through the battery (therefore from convention 3 we have a positive voltage change). The battery has a voltage of 6 so a + 6 is added to our equation. No change from A.
- Next we go through the resistor. The loop direction is now opposite to the nominal current direction (the little arrow drawn to indicate current is drawn anticlockwise, but the loop direction is clockwise). So by convention 4 we write this as positive voltage change.
We use V=IR, the resistance is 60 ohms so we add the term +60I to the equation.
- We have completed the loop, so we set sum of the voltage changes to zero (law 2). We get the equation +6 + 60I = 0.
- Again We solve the equation to find that I = -0.1 amps. The negative value indicates that the conventional current flows in the opposite direction to the nominal or 'arrow' flow (the little arrow that I drew on the diagram).
So this result looks different but it really implies a current going in the same direction. It is just that we have a different convention as to how we define 'positive current'.
Version D
Compared to A we have changed both the loop direction and the nominal current direction.
- As in version B, we go backwards through the battery and have a voltage change of -6.
- The nominal current flow is in the same direction as the loop direction so we right it as a drop of 60I volts.
- This gives us an equation of -6 -60I =0.
- Again this solves to I = -0.1 amps -in other words the flow is in the opposite direction to the arrow in the diagram
About Conventions and Signs
What are we saying here? What does it mean that 'consistency' or 'conventions' will take care of everything? If we say that a current I flowing through a resistance of R causes a voltage drop of IR then we don't care
whether in reality the current is negative (flowing the opposite way) because our equations will correctly indicate a negative voltage drop.
Now we are ready to move to a more advanced example.
Example 2

This is a typical problem. Lets start by labelling the currents.
- Labelling means not only giving a name to them but indicating the direction in which we take flow to be positive (e.g. by drawing a little arrow on the circuit). Remember: this does not have to be the direction that the current is really flowing.
We don't know that yet. So I started (arbitrarily) at the 3v battery. I chose to make I1 go up through the battery. If the real current that passes through the battery goes the other way then I1 will turn out to have a negative value. The same current that passes through the battery also must pass through
the 50 Ohm resistor. I1 is my first unknown.
- When I get to the first node (a in the diagram below) the current divides. I say that as if I really know which way it is flowing -but I don't! I don't know how it splits, but I drew a new unknown current I2 continuing
on through the 200 ohm resistor. So this means that the current going through the 100 ohm resistor (in the downward direction) is I1- I2. We should ask "how much net current is flowing into this node?". The answer should be zero. What do we have? Where I have drawn the current arrows in a
direction leaving the node I must subtract them. So I get I1 - I2 -(I1 -I2), which nicely cancels to zero. If you end up with something that does not cancel to zero then either you have made an error or you have an 'extra unknown'. If the flows into the node simplifies to e.g. I4- I5 -I6, then we know
that these sum to zero and thus I4= I5 + I6. In this case we could simply replace all references to I4 by I5+I6. If you obtained something more complicated, no problem. We know from the first law that it sums to zero (I4 -I5 -I6 =0). Ultimately the problem will become one of solving simultaneous equations
and this will be one of them. Let's call equations like this obtained from the first law "node equations". I am going to set up this problem without any node equations. We could, however, set the problem up in a way that
each leg ("arc" would be the mathematical term) has its own variable name for its current, which would be initially unknown. This would mean having a system of 6 rather than 3 variables for this problem. I don't trust myself to solve that by hand. However, I you were writing a computer
program to solve any kirchhoff network then this might be your preferred approach. There are programs which are widely used to simulate proposed circuits such as 'SPICE' and this type of network analysis is at the core of their algorithms.
- Moving on to node b, the current I2 is split into an unknown I3 and a remaining I2-I3. This gives a total current flowing into b as I2 - I3 -(I2-I3) which simplifies to zero.
- At node d We have I2-I3 entering from above and I3 from the battery. So for currents to ballance (using law 1) I2 must flow out to the left.
So we have three unknown currents I1, I2 and I3. Therefore we must have three independent equations to solve for them. As, in this case, we have no 'node' equations these must all come from our second law, which is that the sum of the voltage changes in any loop is zero. Let's call them 'loop'
equations. Common sense says that we must therefore have three loops, they must include all the components. There are additional requirements that a loop can't be a combination of other loops. In practice, working by hand, any three sensible looking loops will produce uniquely soluble equations. Should
they not you can simply chose another loop. Again, these other criteria become important if you are writing software to chose loops and you loop choosing algorithm does odd things.

O.K. So now let's choose loops and set up loop equations.
- My first loop is labelled L1.
- Because of the way I have drawn my loop arrow I go in a positive sense (from the negative to positive) through the 3v battery for a +3 volt change. Because
- Loop direction Li is in the same direction as I1 where it goes through the 50 ohm resistor. Therefore the voltage change is written as MINUS I1*50.
- The 100 ohm resistor has a current of I1-I2 going through it in the same direction as the loop arrow. Therefore the voltage change is written as MINUS (I1-I2)*100.
- That completes the loop giving an equation: 3- (I1*50) - ((I1-I2)*100) = 0
- My Second loop is labelled L2.
- Starting at the 200 ohm resistor: I have current (I2) indicated in the same direction as the loop so the voltage change is MINUS I2 * 200
- Head south through the 300 ohm resistor. Arrow in same direction as loop therefore voltage change MINUS (I2-I3) 300
- There is no resistor on the bottom (between c and D) therefore no voltage change.
- Going up through the 100 ohm resistor the loop is going against the marked current arrow therefore we have voltage change of PLUS (I1-I2)*100.
- We are back to the beginning so we can assemble the equation: -(I2*200) -((I2-I3))*300) + ((I1-I2)*100 =0
- Third loop Starting at 1.5 volt battery
- The loop arrow passes in a positive direction through the battery so we have a voltage change of + 1.5 volts
- The loop arrow passes against the direction of the arrow in the 300 ohm resistor so we have a voltage change of PLUS (I2-I3) *300.
- This gives an equations of 1.5 + (I2-I3)*300 = 0
Lets clean up the equations
Equation 1
3- (I1*50) - ((I1-I2)*100) = 0
-> 150 * I1 - 100*I2 = 3
Equation 2
-(I2*200) -((I2-I3))*300) + ((I1-I2)*100 =0
-> (I1 * 100) -(I2 * 600) + (300 * I3) =0
Equation 3
1.5 + (I2-I3)*300 = 0
-> (I2*300) - (I3*300) = -1.5
Lets solve them
- Add final forms (above) of equations (2) and (3) to eliminate I3 -> 100 I1 - 300 I2 = -1.5. Call this '(4)'.
- Multiply I1 by (2/3) -> 100 I1 - (200/3)I2 = 2 Call this (5)
- Calculate (4)-(5) to eliminate I1 -> -(700/3) I2 = -3.5
- Calculate I2 -> I2 = 3.5 * 3 / 700 = 0.015 amps
- Put this value in (1) 150 I1 - (100 x 0.015 =3
- Find I1: I1 = (3 +1.5)/ 150 = 0.03 amps.
- Put value for I2 into (3): ((0.015 * 300) - (I3*300) = -1.5
- Find I3: I3 = (1.5 + (0.015 *300) )/300 = 0.02 amps.
Check this stuff!
A feature of Kirchhoff problems is that, though the question may ask the current through a particular resistor, the process always gives the full meal deal: all the currents in the circuit (and therefore
all the voltages across resistors). Because the process consists of a huge number of simple steps, the opportunities for simple errors are many. We should mark our currents and voltages and make sure that they really do obey
our the two commandments:

Note that I have copied my values of I1, I2 and I3 to the appropriate places on the diagram. Then I calculated I1-I2 and I2 -I3. So I2-I3 gives a negative value. All values in amps (in pinky red). This means that the current flows in the opposite direction to the 'arrow direction'.
Next I calculated the voltage drops across the resistors as V=IR. I indicated them in blue or green. I did not give the signs of the voltage change. However obviously the voltage must drop in the direction of the actual current flow.
The current flows in the 'arrow direction' except in the case of the 300 ohm resistor. So I flagged this by making the 1.5 value green. We can now check that we have a solution by checking that voltage changes in any loop that we chose sum to zero.